Pembelajaran Penguatan Numerasi untuk Mapel Non Matematika (Bagian 1)

Pembelajaran Penguatan Numerasi untuk Mapel Non Matematika

Pengantar

Permasalahan 1

Sebelumnya, perhatikan soal berikut.¹ 

Di bawah ini adalah 3 tower yang memiliki tinggi berbeda dan tersusun dari dua bentuk yaitu bentuk segi-enam dan persegi panjang.  Berapa tinggi tower yang paling pendek tersebut?

Ada berapa cara untuk bisa menyelesaikan soal tersebut?

Dari hasil diskusi dengan teman-teman, setidaknya ada 3 cara.

Cara pertama

Perhatikan gambar sebelah kiri. Tower tersebut dapat dibagi menjadi 3 bagian yang sama, yaitu susunan persegi panjang dan segi enam sebanyak 3x. Artinya susunan persegi panjang dan segi enam tersebut tingginya adalah 21 m/3 = 7 meter.

Sekarang perhatikan gambar yang tengah, ketika susunan 1 buah persegi panjang dan 1 buah segi enam tingginya 7 m, maka kita bisa melihat bahwa tower kedua ini terdiri dari 2 persegi dan 2 segi enam yang totalnya setinggi 14 meter. Sehingga tinggi segi enamnya (sisa bangunnya) adalah 19 m - 14 m = 5 m.

Sehingga dapat diketahui bahwa tinggi persegi panjangnya adalah 2 persegi panjang + 3 segi enam = 19 m, atau 2 persegi panjang = 19 m - 3 x 5 m = 19 m - 15 m = 4 m. Jadi tinggi persegi panjang tersebut adalah 4m/2 = 2 meter.

Sekarang perhatikan tower yang sebelah kanan. Dengan mudah dapat diketahui tingginya adalah 2 persegi panjang + 1 segi enam = 2 x 2 m + 5 m = 9 m.

Cara kedua

Perhatikan gambar paling kiri dan tengah. Kalau dikurangkan keduanya diperoleh :

(3 segienam dan 3 persegi panjang) - (3 segienam dan 2 persegi panjang) = 1 persegi persegi panjang = 21 m - 19 m = 2 m.

Dari gambar yang kiri didapatankan bahwa tingga 1 pasang segi enam, persegi panjang = 21/3 = 7 m. Sehingga tinggi tower yang paling kanan adalah tinggi 1 pasang segi enam, persegi panjang + tinggi persegi panjang = 2 m + 7 m = 9 m.

Cara ketiga

Dengan memisalkan tinggi segi enam = x dan tinggi persegi panjang = y, sehingga diperoleh  persamaan :

3x + 3y = 21 atau x + y = 21/3 = 7....(Persamaan 1)

3x + 2y = 19 ...(Persamaan 2)

Dari persamaan 1 dan 2 diperoleh :

3x + 3y = 21

3x + 2y = 19

..................... - 

y = 2

sehingga diperoleh

x + y = 7

x + 2 = 7

y = 7 - 2 = 5

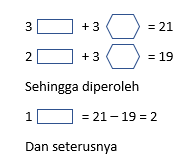
Begitu seterusnya

Soal itu juga dapat diselesaikan dengan cara menggambar langsung sebagai berikut :

Atau dengan mengelompokkan kedua jenis bangun tersebut, siswa pun bisa mengerjakan dengan cepat dan tepat.

Artinya banyak sekali cara yang bisa dilakukan untuk menyelesaikan soal tersebut. 

Dan dari berbagai jawaban tersebut, maka kita bisa mengelompokkan ada yang menggabungkan kemampuan visualisasi, ada yang berbasis teks, ada yang membutuhkan bantuan simbol dan lainnya. Atau secara sederhana ada yang matematis banget ada yang tidak.

Permasalahan 2

Ada 10 orang yang sedang menunggu taksi. Jika setiap taksi mampu membawa 4 orang, berapa taksi yang dibutuhkan?

A. 2

B. 2,5

C. 3

D. 4

Jika diberikan pilihan seperti di atas, manakah jawaban yang dianggap paling tepat.

Secara hitungan matematika dibutuhkan taksi sebanyak 10/4 = 2,5. Meskipun demikian tentunya jawaban tersebut tidak bisa diterima. Jika menjawab membutuhkan 2 taksi, mungkin jawaban yang dipaksakan. Dengan setiap taksi membawa 5 orang maka ada 1 orang yang diselipkan atau dipangku.

Jika menjawab 4 boleh jadi dengan asumsi komposisi penumpangnya 2, 2, 2, 4 atau 3, 2, 3, 2 atau bahkan 4, 4, 1, 1 dan seterusnya. Kenapa kok 1, ya karena ada yang ingin sendirian naik taksinya.😀

Jelasnya, jika jawabanya dibutuhkan 2,5 dapat diasumsikan yang menjawab itu bisa menghitung matematika tetapi numerasinya rendah.

Numerasi atau numerasi matematika ini merupakan kemampuan untuk mengaplikasikan konsep dan keterampilan matematika untuk memecahkan masalah praktis dalam berbagai ragam konteks kehidupan sehari-hari. Termasuk di sini adalah kemampuan untuk menganalisis dan menginterpretasi informasi kuantitatif yang terdapat di sekeliling kita yang ditampilkan dalam berbagai bentuk (grafik, tabel, bagan, dsb.). Hasil dari analisis dan interpretasi itu digunakan untuk memprediksi dan mengambil keputusan (Kemendikbud, 2017).² 

Permasalahan dalam kehidupan keseharian banyak yang terkait dengan numerasi matematika, misalnya untuk menentukan kapan belanja yang paling hemat dengan adanya berbagai variasi tawaran diskon sebuah minimarket. Kasus lain misalnya menentukan ukuran tanah yang dibutuhkan untuk membangun rumah dengan spesifikasi tertentu.

Permasalahan tersebut tidak melulu dialami oleh orang yang belajar matematika tetapi dialami oleh semua orang. Dalam pembelajaran di sekolah, siswa pun mengalami hal sama, yaitu menemukan berbagai permasalahan di berbagai mata pelajaran yang membutuhkan literasi numerasi atau numerasi itu.

Sehingga, menjadi kewajiban guru apapun mata pelajaran yang diampunya untuk lebih memfokuskan dengan konten/materi yang mengandung unsur numerasi. Misalnya, penghitungan zakat pada PAI, grafik dan skala pada IPS, detak jantung pada Penjasorkes, pola gerak lagu pada Seni Budaya dan sebagainya.

Demikian postingan ini sebagai pengantar mengenai penguatan numerasi untuk mapel non matematika. Nanti akan dibahas lebih detil pada postingan selanjutnya.

¹ Harianto Setiawan, dkk, Soal Matematika Dalam PISA Kaitannya Dengan Literasi Matematika dan Keterampilan Berpikir Tingkat Tinggi, (Prosiding Seminar Nasional Matematika, Universitas Jember, 19 November 2014), hal. 249-250

²  Dicky Susanto et.al, Inspirasi Pembelajaran yang Menguatkan Numerasi pada Mata Pelajaran PA, IPS, PJOK dan Seni Budaya untuk Jenjang Sekolah Menengah Pertama, (Kementerian Pendidikan, Kebudayaan, Riset, dan Teknologi, 2021), hlm. 2